期待値とは確率と確率変数を掛けた総和を取ったもののことです。簡単にいうと平均値です。
期待値プラス=(長期的に見て)利益がでるプレイ
期待値マイナス=(長期的に見て)損するプレイ
という意味になります。
期待値とは
よくWEB上のポーカーの記事で期待値という言葉を耳にしますが、その後にでてくる式がややこしそうだからよく理解せずに読み飛ばしている人も多いのではないでしょうか。
できるだけわかりやすく解説しますので、読み飛ばさずに期待値とはいったいなんなのか、理解してみましょう。
まず期待値となはなんなのかを簡単に説明します。
サイコロの出目の期待値はいくらか?
サイコロというのは、6つの面でできた立方体で、転がした時にそれぞれの目(面)は6分の1の確率ででます。期待値の計算は確率(発生する確率)と確率変数(今回の場合サイコロに書かれた数字)を掛けたものを全て足したものですから、
(1/6×1)+(1/6×2)+(1/6×3)+(1/6×4)+(1/6×5)+(1/6×6)=3.5
となり、サイコロの出目の期待値は3.5であることがわかります。
つまり、何回も何回もサイコロを振り続ければ、出目の平均は3.5になるという意味です。
ではお金を払ってサイコロをふり、
- 1が出たら10円
- 2が出たら20円
- 3が出たら30円
- 4が出たら40円
- 5が出たら50円
- 6が出たら60円
もらえるゲームがあったとします。もらえるお金は出目の10倍なので、同じ計算で期待値35円です。
このゲームを1回プレイするのにかかる費用が30円の場合、期待値は35円なのでプラス5円となり、儲かるゲーム(期待値プラス)と言えます。
逆に1回40円かかる場合、毎回5円損するゲーム(期待値マイナス)となります。
では少し複雑にして、このサイコロは作りが雑なので、それぞれの目が出る確率にバラつきがあるとします。
それぞれの目が出る確率は
- 1:20%
- 2:15%
- 3:25%
- 4:10%
- 5:10%
- 6:20%
だったとします。合計するともちろん100%です。そしてそれぞれが出た場合にもらえるお金が同じように
- 1:20%:10円
- 2:15%:20円
- 3:25%:30円
- 4:10%:40円
- 5:10%:50円
- 6:20%:60円
だとします、そして確率と確率変数を掛けた総和を式にすると
(0.2×10)+(0.15×20)+(0.25×30)+(0.1×40)+(0.1×50)+(0.2×60)=33.5
となり、期待値は35円から少し減って33.5円になりました。各目が出る確率にバラつきがあったためです。このゲームは33.5円以下でプレイするのであれば期待値プラスであることがわかります。それ以上払うと期待値マイナスです。
オッズの説明の際も書きましたが、これは回数が増えれば増えるほど期待値通りの結果になるので、1回の勝負では損が出ることも多々あります。
期待値とは平均値を出すことでもありますから、平均値に近づくためには、回数を増やさなければなりません。回数が増えれば増えるだけ期待値通りの結果に収束します。
ポーカーでの期待値計算の例
ポーカーの特定のシチュエーションでの期待値計算の例です。
プリフロップでのオールインを受けるかどうか
5人全員が30BB持っているリングゲームで、ルースなMPがオールインしました。
BBのあなたまでフォールドでまわってきて、ハンドを見るとAKsでした。
ここでコールするのが期待値プラスなのかマイナスなのかを計算してみます。
もし勝った場合、60ドルのポットがあなたのものになります。
投資額(コールして出す額)は30BB、得られる総額は自分の出したチップと相手の出したチップの合計の60BB(確率変数)、というのはわかっていますが、勝率(確率)がわからないと、計算式にはできません。
つまり相手のハンドがなんなのかわからないと勝率(確率)も導きだすことができず、式にできません。
よって相手のハンドを仮定して式を作ります。
ルースプレイヤーのオールインなので、ハンドレンジは、全てのポケットペア、ATo+、KT+、QJ+とします。
わかりやすくするため、それぞれのハンド予想に対するAKs勝率を、
- 相手のハンドがAAの場合の勝率は12%
- KKの場合の勝率は34%
- それ以外のポケットの勝率は一律50%
- ドミネートしている場合は一律73%
- それ以外は一律66%
とします。さらに、相手が上のどのハンドを持っていそうかの確率を
- AAの確率をa
- KKの確率をb
- それ以外のポケットペアの確率をc
- ドミネートしているハンドの確率をd
- それ以外のハンドの確率をe
とした場合の式は
(60×0.12a)+(60×0.34b)+(60×0.5c)+(60×0.73d)+(60×0.66e)=期待値
となります。しかしこれだけでは具体的な数値はまだでません、abcdeにそれぞれ仮定した数値を入れます。
相手が
- AAの確率を10%
- KKの確率を10%
- AA、KK以外のポケットの確率を40%
- Axの確率を30%(ドミネートしているハンド)
- それ以外の確率を10%
と仮定します。すると式は
(60×0.12×0.1)+(60×0.34×0.1)+(60×0.5×0.5)+(60×0.73×0.3)+(60×0.66×0.1)=34.86
となり、あなたは30BBの参加費で期待値34.86BBのゲームに参加することになります。
参加費である30BBを期待値から引くと期待値+4.86、よって期待値プラスと言えますね。
しかしこんな式を覚えるのは面倒ですし、プレイ中に毎回計算などできません。
そこで実戦でのプレイに役立つように、簡略化した式にしてみます。
AKsというのは相手がAAかKKの場合は著しく不利、それ以外の場合勝率は60%前後あることになりますから、すこし強引ですが、わかりやすく2種類の結果にします。
- 相手がAAかKKの場合の勝率を一律20%、相手が持っている確率をx
- 相手がAAかKK以外の場合の勝率を一律60%、相手が持っている確率を1-x
とします。また、期待値が投資額30BBよりも大きくなるためのxを導くため、
30≦(60×0.2x)+(60×0.6(1-x))
という式にします。この式を解くと
x≦0.25
となり、相手がAAかKKの確率が25%以下であれば期待値プラス、25%以上あるのであれば期待値マイナス、と言うことができます。
この式はヘッズアップの場合にしか意味がありません。
相手が一人で、そのハンドがAAかKKなのか、それ以外なのか、という状況を式にしたものなので、相手が二人いた場合は、ハンドの仮定がより複雑になるためです。
プリフロップ以外での期待値計算
期待値を計算するシチュエーションは、プリフロップだけでなく、ラウンドが進んでからでも発生します。
例えば、
「ヘッズアップで相手がロックと呼ばれるスーパータイトプレイヤーの場合、自分がオリジナルレイザーなのであればCBは必ず打つほうが期待値プラスになる」
「フラッシュ目があるボードでストレートを引いた場合、リバーでベットしたほうが期待値プラス」
という使われ方をします。
相手がタイトならCBは毎回うったほうが期待値プラス?
「ヘッズアップで相手がロックと呼ばれるタイトプレイヤーの場合、自分がオリジナルレイザーなのであればCBは必ず打つほうが期待値プラスになる」という仮定を式にして検証してみます。
まず、以下の設定を前提条件とします。
- あなたはプリフロップで3倍レイズしている(レイズメイク3BB)
- フロップ時点でのポットはブラインドを加味して8BBとする
- ロックはヒットすればコール(もしくはレイズ)、何もヒットしなければフォールドする
- CBは3BBベットする
まずロックがフロップでヒットする確率ですが、ランダムハンドがフロップでヒットする確率は32%あります。つまり残りの68%はノーヒットであり、あなたのCBに対してフォールドします。
あなたがCBをうって相手がフォールドした場合に得られる利益はプリフロップで相手が出した3BBです。
あなたがCBを打って相手がコール(もしくはレイズ)し、結果あなたが負けて失うのはプリフロップでうった3BBとフロップのCBでうった3BBの計6BBです。
よって、毎回CBを打つとすると、68%の確率で3BBの利益を得て、32%の確率で6BBを失うことになり
(0.68×3)+(0.32×-6)=0.12
となり、これだけでもやや期待値プラスとなります。
しかし、上記条件は、相手がヒットした場合あなたが必ず負けるという前提で計算していいます。
しかし実際には、相手がヒットして、且つあなたもヒットして勝っているパターンも存在します。その確率を5%と仮定した場合の式は
(0.68×3)+(0.05×3)+(0.28×-6)=0.51
となり、期待値はさらに上昇します。
これが、相手が非常にタイトなプレイヤーだった場合、CBを打つ頻度を上げれば期待値プラスとなる根拠になります。
ヒットしないと打てないという初心者プレイヤーは、この根拠を頭に入れて、恐れずにCBを打てるようになるべきでしょう。
ただし、繰り返しますが以下の条件にあてはまる場合だけです。
- 自分がオリジナルレイザーである(A持ちかポケットであるという主張。相手がノーヒットの場合降りやすい。)
- ヘッズアップである(2名以上を相手にしてむやみにCBを打つのは危険。)
- 相手はタイトである
ストレート引いたけどフラッシュに負けてるかも・・・でも打つべき?
次に「フラッシュ目があるボードでストレートを引いた場合、リバーでベットしたほうが期待値プラス」を式にして検証してみます。
全員100BBを持った5人でのリング、あなたはMPから
 で3BBにレイズ、タイトなBTNのみコールしてフロップに進みます。ポットは8BBです。
で3BBにレイズ、タイトなBTNのみコールしてフロップに進みます。ポットは8BBです。
フロップ:


あなたはオープンエンドになりました、CBを打ちます。
あなたベット4BB→BTNコール(ポット16BB)
相手はコールしてきました、フラドロ、ポケット、Qヒットなどいろいろ想定できます。
ターン:
あなたはストレートを手にしました、フラドロを引きにきている可能性もあるのでハンドをディフェンスするためにベットします。
あなたベット10BB→BTNコール(ポット36BB)
BTNはコールしました、フラッシュドローなのかそれ以外なのかまだ不明です。
リバー:
7sは相手にフラッシュを完成させた可能性があります。
ここでポジションのないあなたの選択肢は
- チェックコール(チェックして相手がベットしてきてもコールする)
- チェックフォルド(チェックして相手がベットしてきたら降りる)
- バリューベットorブロックベット
という3択になりそうです。
相手のハンドレンジはタイトプレイヤーなため、77~QQ、AT+、KJs+、QJsと想定します。
KK、AAはプリフロップで3ベットしているはずなので除外します。
フラッシュドローのあるフロップでBBはジャストコールしていますから、セットはなさそうです。
よって、リバーの時点で相手は、フラッシュ完成、ポケットペア、Qヒット、Kヒット、2ペア、というのが本線になります。77のセットはまずないでしょう。
あなたのストレートはフラッシュ以外には勝っています。
相手のハンドを20%をフラッシュ完成、80%をそれ以外だと想定します。
チェックコールした場合の期待値
- フラッシュで相手がベットする確率を1(100%)
- フラッシュ以外で相手がベットする確率をx
- フラッシュ以外で相手がチェックする確率を1-x
- ベットする額をy
とします。
相手がフラッシュだった場合、ポットの36BBはそもそも失っていたものなので損害と考えず、相手がフラシュでのベットに対してコールした場合、相手のベットした分だけ損することになります。
フラッシュ以外の場合、元々得られる36BBに加えて、相手のベット分だけコールすることで利益がでます。よって式は
0.8×(x×y+(1-x)×0) + 0.2×-y=期待値
という式になります。これは左から説明すると
0.8=相手がフラッシュ以外である確率(80%)
x×y=相手が(x)の確率でフラッシュ以外でベットし、yの分利益になる
(1-x)×0=相手が(1-x)の確率でフラッシュ以外でチェックし、チェックチェックで利益はプラスマイナス0
0.2=相手がフラッシュである確率(20%)
-y=相手がベットしy分だけ、あなたはコールするので損する
という意味になります。
ここでxとyという2つの変数がありますから、どちらかを仮定するために、相手のベット額(y)をポットのハーフの18BBとします。また、期待値がプラスになるための式にするため、0≦となるように計算式にすると
0≦0.8×(x×18+(1-x)×0)+ 0.2×-18
0≦14.4x-3.6
という式になり、xが0.25以上、つまり相手が25%以上の確率でフラッシュ以外のハンドでベットしてくるのでであれば期待値はプラスになります。
チェックフォルドした場合
- フラッシュで相手がベットする確率を1(100%)
- フラッシュ以外で相手がベットする確率をx
- チェックする確率を1-x
とします。相手がベットした場合フォールドするため、相手のベット額はいくらでも関係ありません。
これは、相手がフラッシュでベット、もしくはフラッシュ以外でチェックすれば、本来の結果通りになり期待値はプラスマイナス0ですが、フラッシュ以外でベットした場合、本来得られるはずだった36BBを失うことになります。つまり、期待値マイナスになることはあっても、プラスにはならなさそうです。式は
0.8×(x×-36+(1-x)×0) + 0.2×0=期待値
となります。
0.8=相手がフラッシュ以外である確率(80%)
x×-36=相手が(x)の確率でフラッシュ以外でベットしあなたはフォールドするので、本来得られるはずの36BBの分損になる
(1-x)×0=相手がフラッシュ以外でチェックする確率(1-x)で、利益はプラスマイナス0
0.2=相手がフラッシュである確率(20%)
0=相手がフラッシュなのであれば、36BBはもともと得られないはずだったものなので、損にはならない
この期待値がプラスになるために
0≦0.8×(x×-36+(1-x)×0) + 0.2×0
という式にすると
0≦-28.8x
となり、やはりx(相手がフラッシュ以外でベットする確率)が限りなく0に近くても期待値プラスにはどうやってもなりません。
バリューベットorブロックベットした場合
- あなたのベット額を13BB(ポットの3分の1)
- 相手がフラッシュでレイズする確率を1(100%)
- 相手がフラッシュ以外でコールする確率をx
- 相手がフラッシュ以外でレイズする確率をy
- 相手がフラッシュ以外でフォールドする確率を1-x-y
- レイズされればフォールドする
とします。
これは、相手がフラッシュであれば打った13BB分損することになります。
相手がフラッシュ以外で、コールするとうった13BB分利益に、フォールドすると利益はプラスマイナス0、レイズされるとあなたはフォールドなのでうった分と本来得られるはずの36BBを損することになります。式にすると
0.8×(x×13-y×(36+13)+(1-x-y)×0)+ 0.2×-13
となります。
0.8=相手がフラッシュ以外である確率(80%)
x×13=相手が(x)の確率でフラッシュ以外であなたのベットにコールするので、13BBの分利益になります
y×(36+13)=相手がフラッシュ以外でレイズする確率(y)で、あなたはフォールドするので、打った分と、本来得られるはずの36BBを損します
(1-x-y)×0=相手がフラッシュ以外でフォールドする確率(1-x-y)で、あなたは本来得るはずの36BBを得るだけなので利益はプラスマイナス0です。
0.2=相手がフラッシュである確率(20%)
-13=相手がフラッシュでレイズし、あなたはフォールドするので、打った13BBの分損します
この式でも変数がxとyの2つあるので、相手がフラッシュ以外でレイズする確率(y)を、かなり低いはずなので、5%(0.05)と仮定します。
すると式は
0≦0.8×(x×13-0.05×(36+13)+(1-x-0.05)×0)- 0.2×13
0≦10.4x-4.56
となり期待値がプラスになるのはxが0.44以上の場合、つまり44%以上の確率で相手がフラッシュ以外でコールしてくれるのなら期待値はプラスになります。
各アクションのまとめ
これで3つのパターンの期待値が全てでましたが、チェックフォルドはそもそも期待値はマイナスなので除外します。
チェックコールは
0≦14.4x-3.6となり
相手が25%以上の確率でフラッシュ以外のハンドでベットしてくるのでであれば期待値プラス。
バリューベットは
0≦10.4x-4.56となり
相手が44%以上の確率で相手がフラッシュ以外でコールしてくれるのなら期待値プラス。
であることがわかりました。では
- あなたがチェックして相手がフラッシュ以外でベットしてくる確率
- あなたがベットして相手がフラッシュ以外でコールする確率
の実際の確率はどれくらいになるでしょうか?
常識的に考えるなら、あなたがリバーでチェックすれば、相手がフラッシュ以外であれば、このボードならそのままチェックしてショーダウンとなるのではないでしょうか。つまり、フラッシュ以外で、あなたのチェックにベットする人は2ペアやセット、もしくはブラフの頻度が高い人です。25%以上もフラッシュ以外でベットことがあるでしょうか?多くみつもっても20%程度でしょう。
また、あなたがリバーでベットして、相手がフラッシュ以外の場合、それまでコールしてついてきたトップヒットや2ペアのプレイヤーはポットの3分の1のベットであれば高い確率でコールするでしょう。仮に80%はコールするとした場合、バリューベットの場合の期待値は
10.4×0.8-4.56=3.76
という期待値なのに対し、チェックコールで同じ3.76の期待値になるためには
14.4x-3.6=3.76
となり、xは0.51、つまり51%以上の確率でフラッシュ以外のハンドでベットしてくる必要があります。
51%以上の確率でこのボードでフラッシュ以外がベットしてくるでしょうか?おそらくないでしょう。
よって、バリューベットのほうが期待値は高くなります。
さて、この期待値計算ですが、相手がフラッシュかそれ以外かの確率を、冒頭で20%と80%とざっくり計算しました。しかしこの確率が大きく変わるのであれば、結論も変わってきそうです。
そもそも今回の例は、
- ポジションがない
- 相手にハンドが勝っているか負けているか不明
- 相手が勝っている場合100%ベット(もしくはレイズしてくる)
- リバーでどういうアクションが期待値が最も高いか
という状況ですから、相手がフラッシュかどうか、だけに限らずいろいろなハンドの場合に使える計算です。
そこで、汎用的に使える計算機を googleスプレッドシートで作ってみました。
ポジションがない時のアクション別期待値計算表(現在削除しています)
今回の例で出てきた変数は全て変えれるようになっています。
ただし、そこまで汎用的でもありません。
今回の例では相手がフラッシュの場合100%ベット(もしくはレイズ)する、としているので、相手のほうがハンドは強いが相手がベットしないパターンは計算できません。
たとえばフラッシュ目のあるボードで、あなたがセットで相手がストレートの場合などです。あなたがチェックして、相手もフラッシュを恐れててチェックする、ということがありえます。
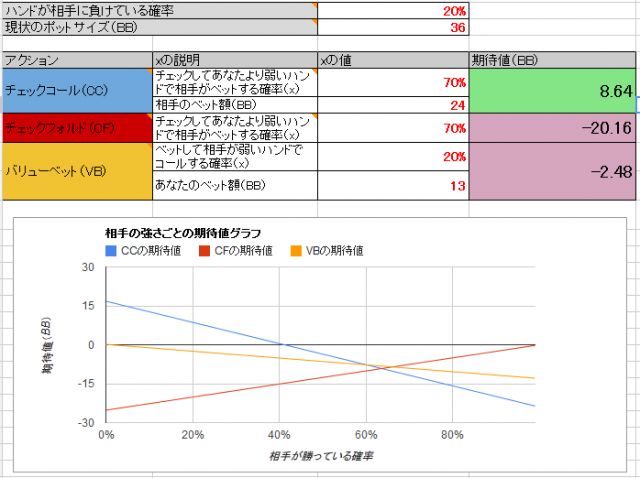
とりあえず、今回の例を数値を入力して出た結果が以下です。(画像はクリックで拡大します。)
相手がフラッシュ(あなたが負けている)の確率が20%、その他ポットサイズや相手がベットする額、コールする確率などを上記のようにすると、バリューベットが最も期待値が高くなります。
これらの数値の、相手がフラッシュの確率を1%~100%まで変化させた場合の期待値の変動をグラフにしたものが以下です。(画像はクリックで拡大します。)
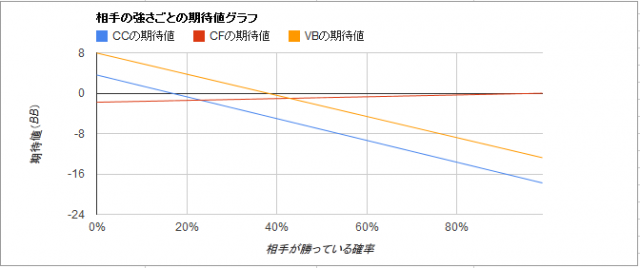
このグラフを見れば、相手がフラッシュ(自分よりも強いハンド)の確率が38%を超えると、何をしても期待値はプラスにならないことがわかります。また、相手がフラッシュの確率が43%を超えると、チェックフォルドが最もマシな期待値になります。(それでもマイナスでプラスにはなりません)
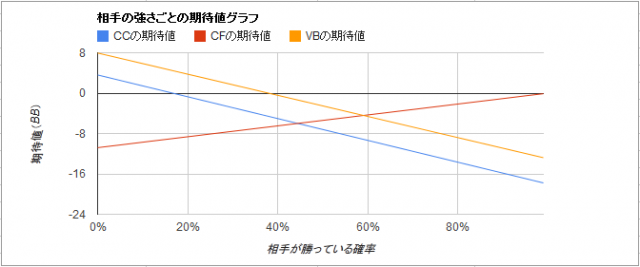
もし相手が、トップヒットや2ペアでフラッシュを装うブラフが多々ありそうなら、相手がフラッシュ以外でベットする確率(チェックしてあなたより弱いハンドで相手がベットする確率(x))を上げます。これを30%まで上げてみると、グラフは以下のようになります。
ブラフされる確率が上がる分、チェックフォルドの期待値が下がりましたね。しかしそれでも相手がフラッシュの確率が58%を超えるのであれば、チェックフォルドがもっともマシな数値になります。
最後に、相手がブラフしまくる人で、あなたがチェックすると、フラッシュならもちろん100%ベット、それ以外の場合でも70%の確率でベットしてくるようなプレイヤーで、さらにあなたがベットすると、かなりの確率でフォールドしてしまうような(つまりクソハンドで入ってくるルースプレイヤー)場合は以下のようになります。
バリューベットは、相手がフラッシュの場合だけコール(もしくはレイズ)されるので期待値プラスになりません、チェックフォルドも、ブラフされてしまう可能性が高いので期待値は低くなります。よって、チェックコールでブラフキャッチが最も期待値が高くなります。それでも相手のフラッシュの確率が66%を超えるのであればチェックフォルドがまだマシですね。
相手が超ブラファーなのであれば、チェックコールしてブラフキャッチ、フラドロを頻繁に引きにくるようなプレイヤーならチェックフォルド、という方針がベストのようです。
まとめ
こうした期待値計算は、プレイが数学的に正しいのかどうかを裏付けてくれる大事なツールとなります。
もちろん確率や可能性といった確定的ではない数値が入るため、期待値計算が100%正しいとは言えないこともありますが、ほぼだいたいのプレイに対して正しいか正しくないかの指針を示してくれます。





コメント 名前とメアドは必須ではありません
フラッシュの確率が20%というのはどうやって計算したんですか?
追記です。相手のレイズが5%というのはどのハンドでレイズしてくると考えて5%なんですか?
コメントありがとうございます。2つのご質問にまとめてお答えします。
フラッシュの確率についてですが、この数値はあくまで仮定です。1%の場合もあれば99%の場合もあると思います。この記事内では、20%と仮定しただけで、大事なのはその数値ではなく、20%と仮定した場合の「結果」です。フラッシュの確率を1%~100%まで変化させた場合のグラフも掲載しているように、どの程度のパーセンテージであれば、どういったアクションが期待値プラスなのか、という考え方を知ってほしいために書いています。
レイズの確率が5%も同じです。仮定しているだけです。
どのようなハンドでレイズしてくるか、ということを考えるのは大事なことですが、それは実際にプレイしている相手やシチュエーションによって様々でしょう。なので、プレイヤーは5%という確率を自分で調整するべきです。
どちらもそうですが、20%や5%という数値は変動するものです。この記事は、どういった数値であればどういうプレイが最適か、それぞれのプレイヤー自身で考えていただくための、考え方の助けになればと思い書いたものなので、このページに書かれている数値に固執しないでください。
相手がタイトならCBは毎回うったほうが期待値プラス?
の項目について質問です。
(オリジナルレイザーである)自分がフロップでCBを打つことでロックがフォールドした場合の利益は、フロップでロックが出した3BBということでしたが、そもそもロックがフロップで3BB出すという状況は、ロックがフロップで3BBベットした場合、もしくは自分がフロップで3BBベットした後、ロックがコールしたというこの二つの場合しか考えられず、しかもこの二つの状況はどちらも鮫肌さんが述べられている勝負の状況と矛盾してしまっています。
よって、フロップにおいて自分のCBによってロックがフォールドした時に得られる利益は、フロップでロックが出した3BBではないと思います。
状況の数え漏らしまたは僕の考え方が間違っているのだと思うのですが、ぜひ検討して考え方のアドバイスをいただけると嬉しいです。
コメントありがとうございます。
今記事本文を確認したところ「あなたがCBをうって相手がフォールドした場合に得られる利益はフロップで相手が出した3BBです。」というのは間違いで、本来は「あなたがCBをうって相手がフォールドした場合に得られる利益は”プリフロップ”で相手が出した3BBです。」が正しい文章です。
おそらくこの間違いで、勘違いをされたのではないでしょうか。申し訳ありません。記事のほうは、さきほど修正いたしました。